Impact of load balancing on parallel performance with Haar wavelets angular adaptivity

Abstract

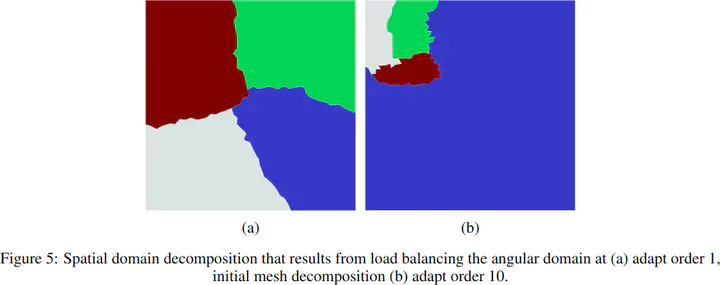
This paper tests the performance gain of performing load balancing with angular adaptivity, that has been discretised using Haar wavelets. Load balancing on highly refined angular meshes resulted into a reduction in the runtime of approximately 50% on a local machine. The time spent load balancing was found to be proportional to the number of unknowns of the problem, with the rate of the proportionality being dependant on the number of processing cores used. Strong scaling performance of 97% was achieved in 240 cores, dropping to 50% for 480 cores, for a mesh of 405,000 triangular elements. The ratio of nodes to halos indicates that as we adaptively refine, the load balancing algorithm produces an increasing number of partitions with fewer nodes and larger halos. Hence, destroying parallel scaling by performing communications instead of a solving the linear system.