Reentrant melting and multiple occupancy crystals of bounded potentials: Simple theory and direct observation by molecular dynamics simulations

Abstract
Aspects of the phase coexistence behavior of the generalized exponential (GEM-m) and bounded versions of inverse power potentials (BIP) based on theory and Molecular Dynamics (MD) simulation data are reported. The GEM-m potential is $\phi(r)=\exp(-r^m)$, where $r$ is the pair separation and $m$ is an adjustable exponent. A simple analytic formula for the fluid-solid envelope of the Gaussian Core Model (GCM) which takes account of the known low and high density limiting forms is proposed and shown to represent the simulation data well. The BIP potential is $\phi(r) = 1/(a^q+r^q)^n/q$, where $a$, $n$, and $q$ are positive constants. The BIP potential Multiple Occupancy Crystal (MOC) or cluster crystals are predicted to form when $q>2$ and $a>0$, for $n>3$, which compares with the corresponding GEM-m condition of $m>2$. Reentrant melting should occur for the BIP potential when $q \leq 2$ and $a>0$. MD simulations in which the system was gradually compressed at constant temperature using the BIP potential produced cluster states in the parameter domain expected but it was not possible to establish conclusively whether a multiply occupied crystal or a cluster fluid had formed owing to assembly structural fluctuations. The Random Phase Approximation reproduces very well the BIP MD energy per particle without any discontinuities at the phase boundaries. The Lindemann Melting Rule (LMR) is shown analytically to give a more rapidly decaying reentrant melting curve boundary than the so-called Melting Indicator (MI) empirical melting criterion which has also been investigated in this study. The MI model gives a better match to the high density phase boundary for small $m$ and $q$ values.
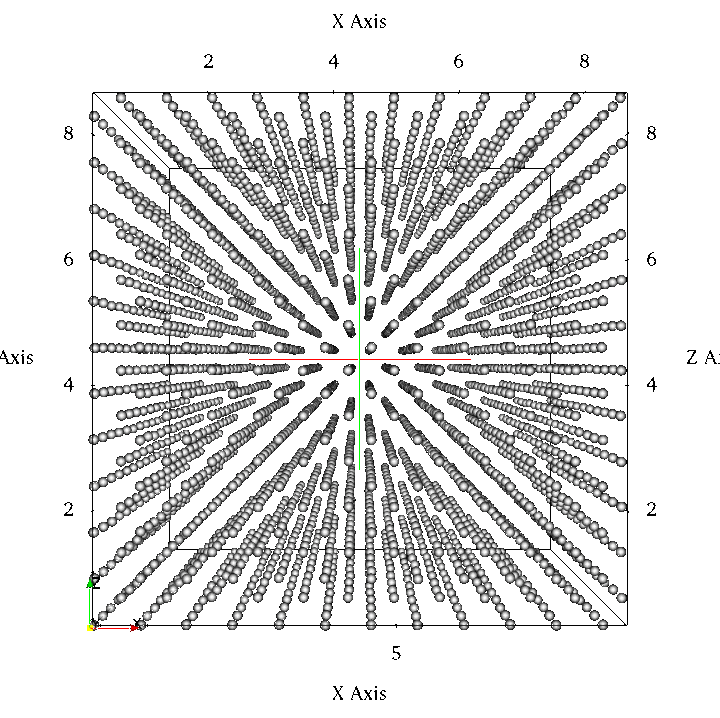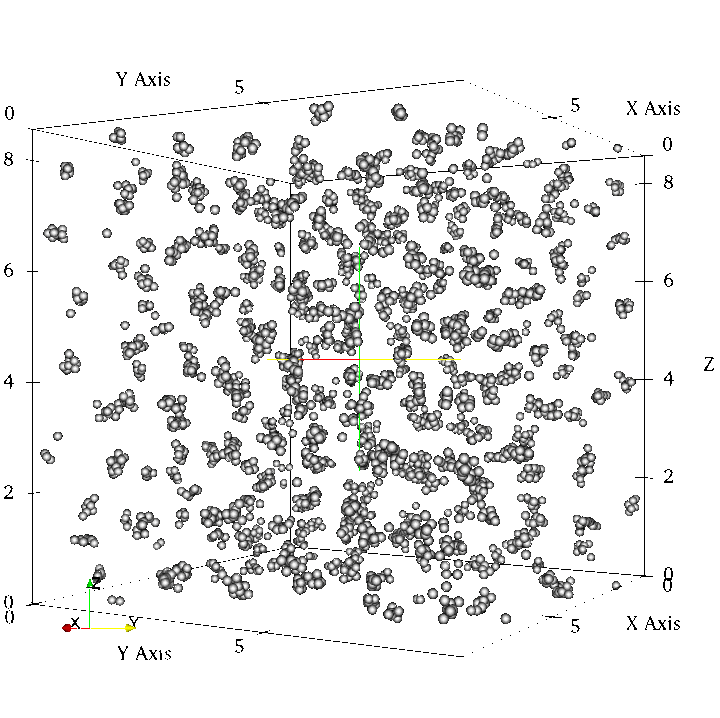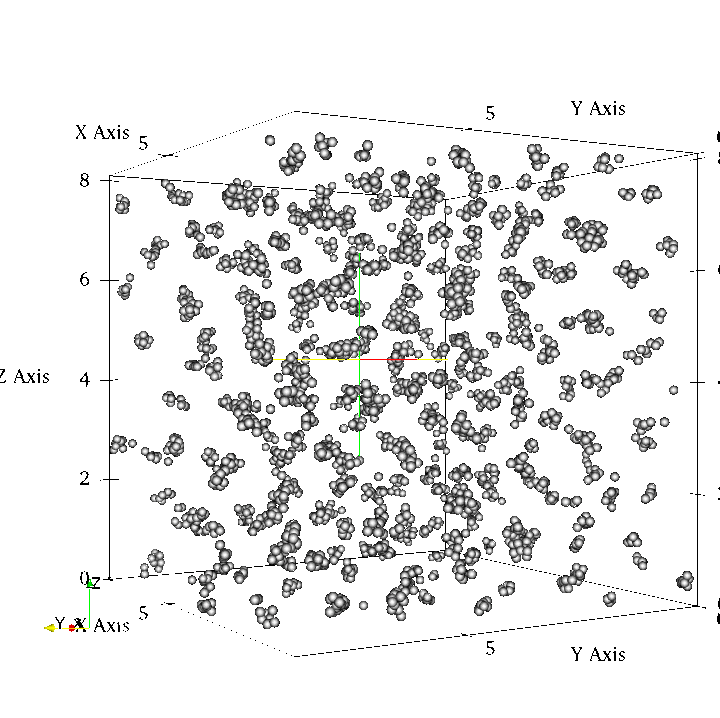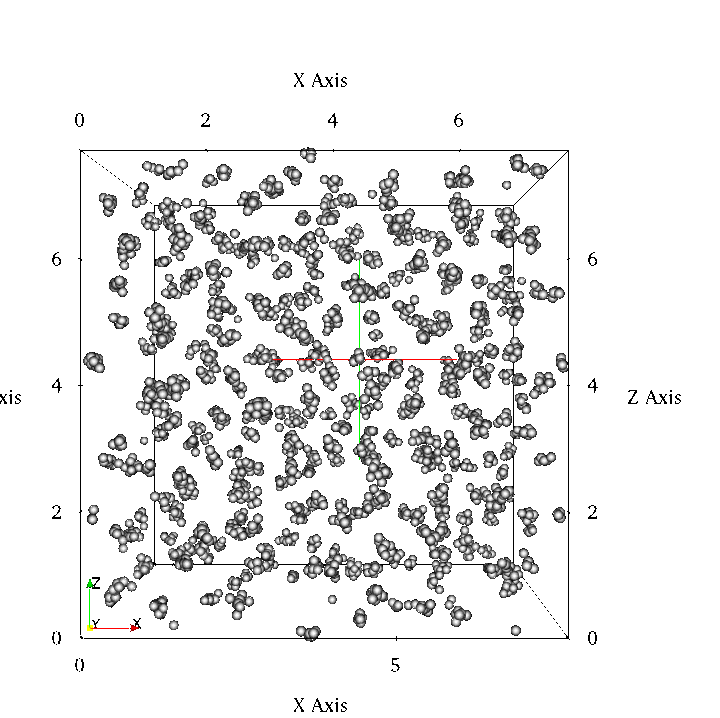
Visualisation of crystals forming in a fluid using a Generalized exponential
(GEM-m) pair potential with m = 4 at a temperature of T = 0.4
using 3456 particles.