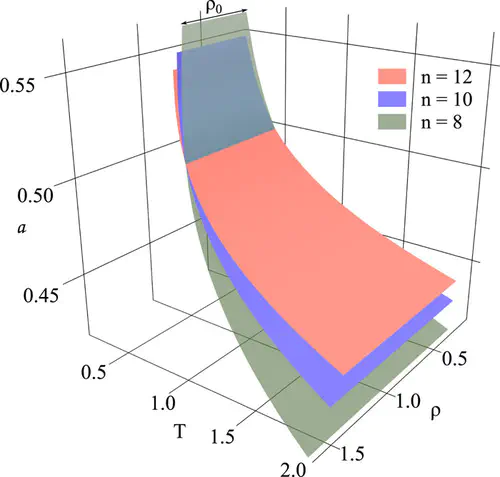
 Theoretical isomorphic surfaces where a BIP fluid has identical statistical properties with varying densities $\rho$, temperatures $T$ and smoothening parameters $a$.
Theoretical isomorphic surfaces where a BIP fluid has identical statistical properties with varying densities $\rho$, temperatures $T$ and smoothening parameters $a$.
Abstract
The bounded inverse power (BIP) interaction pair potential, $\phi(r) = 1/(a^q + r^q)^{n/q}$, where a and the exponent, $n$, are constants which control the interaction softness, $q$ is a positive integer, and $r$ is the pair separation, is shown to exhibit isomorphic scaling as does the well-known inverse power potential, i.e., where $a = 0$. If $T$ is the temperature and $\rho$ is the number density of particles, two state points are isomorphic if a reference state, $\rho_{0}$, $T_0$, $a_0$ and another state, $\rho$, $T$, a are related through the relationships $\rho^{n/3} / T = \rho^{n/3}{0} T{0}$ and $a = a_{0} (\rho_{0} / \rho)^{1/3} = a_{0} (T_{0} / T)^{1/n}$. The potential form is therefore density dependent along an isomorph. Molecular dynamics simulations and solutions of the Ornstein-Zernike integral equation for $q = 2$ demonstrate the existence of isosbestic points (IBPs) in the radial distribution function and structure factor for 6 $\leq$ n $\leq$ 18 and a wide range of a and $\rho$ values. For the BIP potentials with not too small a values and over a wide density range, the IBP distance is insensitive to the number density and is equal to the distance, $r_T$ , defined through $\phi(r_T) = T$. For exponential potentials of the general form, $\phi(r) = C \exp(−r^{m})$ with $1 \leq m \leq 3$, there are also IBPs which are at $r$ values that are typically ∼10-15% larger than predicted by the formula for $r_T$. Published under license by AIP Publishing. https://doi.org/10.1063/1.5089491